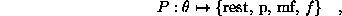MIMI and the Illuminati: Notes
Ralph Abraham, Peter Broadwell, Ami Radunskaya
MIMI PHOTOS
Biographies
Back to MIMI Home Page
Abstract:
Upon the invitation of the Lindisfarne Association and the
Cathedral Church of St. John the Divine in New York City, a concert of
audiovisual mathematics/music took place in the Cathedral Church on
17 October, 1992, at about eight o'clock in the evening. Three computers
and three persons cooperated in the performance. Since then, the ensemble has performed
in a variety of locales and for a variety of audiences. These notes provide
some background and a description of the original event.
1. Visual music and math
Here is a little background on our artistic heritage and orientation.
Visual Music
is a traditional art medium with an extensive, if little known, history.
One can imagine that it played a basic role in the arts and rituals of the cave
cultures of the European epipaleolithic, and the early civilizations of
the Anatolian neolithic. The
cave sanctuaries and rituals of
Minoan Crete, and the derivative
mystery schools of Ancient Greece
may have continued this artistic tradition,
along with its mystical religious
associations. The performances
of Father Castel in Paris of color music
created with candlelight and cloths
were famous in the eighteenth century.
In more recent times, visual music reappeared
in the Theosophical Revival at the turn of
this century. Aleksandr Scriabin intended
Prometheus: The Poem of Fire
(1910) to be accompanied by a light show.
Alexander Wallace Rimington
performed live color music in London
at about this time.
Claude Bragdon and Thomas Wilfred
in New York
created keyboard instruments for the
live performance of color music
in the 1920's.
In the same period, color music compositions
in the form of animated films were laboriously
made by
Arnaldo Ginna and Bruno Corra in Italy,
and Oskar Fischinger in Germany.
In 1936 Fischinger moved to California,
where he continued his work, influencing
John Whitney and others of a major
group of color music film artists
in America.
The live performance of color music
survived in the work of
Mary Hallock Greenewalt in Philadelphia in the 1940's
(she invented the rheostat for her organ),
Charles Dockum in New York and California in the 1950's,
and of course in the Hippie culture of the 1960's.
Traditionally, masters of visual music,
such as Father Castel
or Mary Hallett Greenwalt,
gave performances in silence on
instruments of their own creation.
In the film works of
visual music by
Oskar Fischinger
and by
James and John Whitney,
mathematics was
used as a source of visual musical form
for the first time. In the analog
video synthesizers and fluid cymatic
light shows of the 1960s, visual
music - in partnership with aural music -
ascended to new heights of popularity
and creativity. Our work is further
research in this direction, catalyzed by
rapid advances in computer science
and the mathematics of chaos.
Visual Math
is a new development empowered
by the computer revolution.
Computer graphics has boosted math into an
art medium,
making mathematical objects visible, and
revealing the incredible beauty of
the mathematical landscape.
In the branch of mathematics known as
chaos theory,
massively parallel models called cellular dynamata, or
CDs,
are routinely observed (running on massively parallel
super-computers)
as animated color images.
Both spatial and temporal chaos abound in these morphogenetic
natives of the mathematical landscape.
MIMI (the Mathematically Illuminated Musical Instrument)
was first conceived in a talk
by Ralph Abraham at the
International Synergy (IS) Institute in Los Angeles
on October 7, 1984. Actual
construction of the first model began in July, 1985,
with support from the IS Institute. While this
instrument is not yet complete, simulations
by supercomputers have been circulating on
videotape since 1989. The Cathedral performance
in the Fall of 1992,
the premiere MIMI concert, was an ensemble
of three computers and three humans.
In concert,
the ILLUMINATI TRIO plays visual
music based on CD models in the
supercomputer, and coordinates aural music
based on the same models. The aural
component is enlarged by an obbligato cello line.
The evolution of the
CD models themselves is affected by gestural
input from the three performers.
Beyond the exploration of
computer/visual math/music,
we are fascinated by the resonance between
the two modes. We are extending the domain
of Pythagorean harmony, following
John Whitney, into an audiovisual
and mathematical landscape
2. The Performers
(A) The audio performer
is Ami Radunskaya, Professor of Mathematics
(ergodic theory of dynamical systems)
at Pomona College in Claremont, California. Ami
has worked extensively at the Center for Computer
Research in Music and Acoustics at Stanford University and the
Center for New Music and Audio Technology at the
University of California at Berkeley. She has just
released a piece on the
Centaur Label.
She is also responsible
for the overall composition of the pieces
of this performance.
(L) The linking performer is
Ralph Abraham, Professor of Mathematics
(chaos theory, computation, and applications)
at the University of California at Santa Cruz,
founder there of the Visual Math Project and
Computational Math Program,
and author of
Dynamics, the Geometry of Behavior.
(V) The visual performer is Peter Broadwell, a freelance
software and computer graphics artist. Peter studied
computational mathematics in the Visual
Math Program at the University of California
at Santa Cruz, where he helped create the
software of the Computational Math Lab, earning the
degree of Master of Arts in Computational
Mathematics in 1988. He was for several
years (including the time of the concert)
a member of
the Technical Staff at SGI,
in Mountain View, California, where
he created the IRIS software we are
now using.
3. The Concert Setup
We use three instuments, one for each
performer.
The audio (A) instrument is a Yahama TG77
synthesizer, controlled by the IRCAM/Opcode
program MAX running on a Macintosh computer.
The program MAX receives, processes, and sends MIDI
messages. It is set up to respond to
the V instrument (which generates the animation)
and also to commands sent from
the L instrument, and sent from
performer (A) with her electric cello,
and Zeta MIDI controller.
The video (V) instrument is a
IRIS 4D/440VGXT, a 200 MIPS
graphics workstation on loan from the
manufacturer,
Silicon Graphics, Inc. (SGI).
It runs programs from
the research frontier of chaos theory, the
mathematical theory of nonlinear dynamical systems,
cellular dynamata,
or CDs,
and
iterated endomorphisms
of the plane,
or endos.
Two CDs were featured in the Cathedral
concert: the Brusselator
and the Logistic Lattice,
and two endos : the twisted
logistic and the Henon.
All of these are classics of
the recent research frontier.
These mathematical systems have parameters which
may be manipulated by performer (V).
The SGI IRIS workstation creates the
digital video
stream in real time, that is, as you watch.
Performer (V) sends commands to the IRIS with
Lightning wands, made by Buchla and Associates
of Berkeley, California.
The linking instrument (L) connects the two instruments.
This third computer,
an SGI IRIS INDIGO graphic workstation,
also on loan from SGI, uses
algorithms from
chaos theory to communicate
features of the video (V) to the
audio (A) system.
The algorithms are controlled
by performer (L) by means of
LIGHTNING wands.
4. Mathematics in Music
As in the visual arts, or perhaps even more so, mathematics has played an
enormous role in the creation of musical forms at every level. Music has, in
fact, been defined as ``structured sound'' (see R. M. Schaefer The Art
of Sound), and mathematics provices the richest vocabulary for the
description of structure. The contributions of music to the understanding
of mathematics are perhaps more obscure, but nevertheless present throughout
history. The Pythagoreans made a religion of numbers and their relationships,
and the audification of small integer ratios. The creation of ``just''
harmonic relation, for example octaves, fifths, and fourths, contributed to the
understanding of the mechanism by which sounds themselves were produced - the
creation of standing waves in a string, for example. With the advent of computers,
and in particular of digital sound, the relationship between numbers and
music has become much less subtle and much more intimate: digitally encoded
sound is, after all, a list of numbers. The ear is capable of perceiving
changes in these lists of numbers received at a rate of 40,000 numbers per
second. It is this large band-width that makes the audification of
certain mathematical processes in intriguing: perhaps the ear can detect
patterns which are too long for the eye to process in one pass. In fact,
a heart specialist will sometimes ``listen'' to an electrocardiogram to detect
periodicities and abnormalities that the eye could not: the data is
treated as a time-domain representation of an audio signal, and is run through
a DAC (digital-to-analog converter) so that the physician can hear it: repeating
or periodic patterns can then occasionally be perceived as pitches.
Although the work described here was conceived of and presented as an artistic
rather than a scientific enterprise, the same set-up can be used to shed
light on the mathematical structures themselves. With the visualization
and audification of an evolving mathematical structure occurring simultaneously,
the observer can process more dimensions simultaneously, and hence has
more hope of discovering evidence and justification for any theoretical
conjectures which may suggest themselves. This bidirectionality - the music
as an audification and hence a clarification of the mathematics; and the
mathematics as a musical source - is to me one of the more intriguing aspects of
this work.
It is important to note that music as ``structured sound'' does not necessarily
mean ``ordered'' sound. The structures in question could be stochastic
as well as deterministic. In fact, the particular family of systems presented in this concert
exhibit the full spectrum of behaviour, from the ordered to the chaotic. The creation
and dissolution of order is one of the parameters that is ``played'' during
the pieces.
The use of random processes as a compositional tool goes back at least to
Mozart, who composed a waltz which would now be described as a one-step
Markov process: each measure was a state
of the process, and the probability of another given measure occurring
next depends on the current measure. The choice of which measure would
actually follow a given measure in performance was to be made by rolling an appropriate
(6-sided) die. This waltz of Mozart's can be used to introduce the concept
of a mapping from state space to musical parameter space. The ``state space''
of a process is the set of all possible outcomes of that process. For example,
the process which consists of repeated tosses of a coin outputs heads or tails,
so its state space is the set 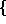 heads, tails
heads, tails 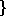 . For Mozart's waltz,
the process (performance) outputs measures one at a time, hence the
state space is the set of all possible measures. He composed and labeled
these measures with the number 1 - 92. For a Markov process, the set
of all possible sequences of states and their relative probabilities is
described by transition probabilities: the likelihood of moving
from a given state to another. In Mozart's score it is shown that there
are only 6 measures which are allowed to follow any given measure, and
one out of these 6 measures is to be chosen ``randomly'', that is with
equal chance of any of the six occurring. Thus the transition probability of going from
measure A to measure B is zero, if B is not one of those 6 measures,
and is 1/6 if it is.
. For Mozart's waltz,
the process (performance) outputs measures one at a time, hence the
state space is the set of all possible measures. He composed and labeled
these measures with the number 1 - 92. For a Markov process, the set
of all possible sequences of states and their relative probabilities is
described by transition probabilities: the likelihood of moving
from a given state to another. In Mozart's score it is shown that there
are only 6 measures which are allowed to follow any given measure, and
one out of these 6 measures is to be chosen ``randomly'', that is with
equal chance of any of the six occurring. Thus the transition probability of going from
measure A to measure B is zero, if B is not one of those 6 measures,
and is 1/6 if it is.
Abstractly, we could describe this process by giving only
these transition probabilities, and by saying we are dealing with a
state space of 92 discrete elements. The performance could then be
described by a mapping, or function, from this state space to
musical space. In the waltz, the mapping associates a number between
1 and 92 with one measure of music, or a short sequence of pitches with their
durations. Notice that this process, though random, does not produce a
random sequence of pitches. All of the pitches are predetermined by the composer.
In fact the ordering of pitches on a small scale, the pitches within
one measure, is also predetermined. This is significant since the direct
mapping of numbers to pitches, which is the naive approach to the audification
of a mathematical process, should be considered as only one of many possibilities, and yet it is the most commonly heard. The application of
mathematical structures in real-time, whether these structures are random
or deterministic, can be applied at any or many of the levels in the
musical hierarchy. Exploration of the range of possibilities is one of the
goals of the MIMI project.
In our pieces, the visual and audio realizations of the mathematical processes
are bound together by virtue of their common origin, but this connection could
be either emphasized by synchronizing noticeable features of the sound and
visuals, or it could be de-emphasized by using mappings which incorporate
varying amounts of delay. Both extremes are displayed in the two examples
discussed below, as well as a range of performer inter-action and improvisation.
5. Two sample pieces
Morphic Resonance
The piece is governed by the Brusselator, a two-dimensional lattice
of oscillators introduced by Ilya Prigogine as an evolution
of Alan Turing's 1952 model for chemical morphogenesis.
An initial pattern chosen by performer L sets off an evolutionary sequence
of images, computed in real time by the super-computer, subject to
parameters chosen by performer V.
This CD (cellular dynamata) evolves relatively slowly, and it suggests
slowly evolving sonic material. Although individual spots vibrate with
swiftly changing colors, the overall image is made up of slowly
spreading regions of color, sometimes made up of many colors, sometimes more or
less monochrome. An attempt to represent these features sonically resulted in the
use of an averaging over many samples rather than requiring a perceptual
change with each numerical value.
Information-theoretic entropy is a measure of complexity
which was adapted from
information theory in the 50's and applied to dynamical systems.
Roughly speaking, it measures the average amount of information required to specify
the next observation. If the process is completely predictable, no information
is required at all, since it is known ahead of time what will happen next.
Hence, predictable processes have zero entropy. Since this entropy
is determined by the infinite future, it is impossible to actually compute
it on the fly from observations of the output of a given process. However,
an extimate can be made by counting the number of different sequences
of digits appearing in a string of a fixed length, and divind the logarithm of
this number by the length of the string:

The higher the entropy, the more complex the stream of numbers.
The MAX patch for this piece estimates the entropy of the process by looking
at sequences of length 127. This number, which we refer to as the
frame entropy, is then fed to another subroutine which creates chords.
The higher the frame entropy, the more dissonant the chord will be.
This is accomplished by adding to the chord pitches which appear later
in a specified harmonic sequence. As soon as one frame entropy is
computed, the first number is deleted, the next number in the series is fed in, and a new frame entropy
is output to the main patch. In MAX this computation does take some time,
and there is some lag between ``what you see'' and ``what you hear''.
The overall harmonic progression is predetermined, but the rate at which
it progresses is also affected by the complexity of the incoming numbers
through the main patch. The timbres are singing voices, and they provide
an accompaniament to an obbligato cello line which follows the evolving
harmonies.
Fruit Fly Fandango
The second selection on the video provides an example of audification
on a larger scale: this cellular dynamata is distinguished by abrupt, almost
periodic changes in the time-series of a given lattice point. In order
to hear this aspect of the evolution of the system, amplitude was
chosen as the dominant perceptual musical parameter. The underlying process
is a two-dimensional array of logistic functions connected by Laplacean
coupling on the torus.
Performer L again
selects two time-series for transmission to the Macintosh. Each of these
time-series is visualized by mapping one variable to a color spectrum.
The same variable, which we'll denote by 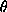 , is mapped to one
of four amplitudes by rounding it off to the nearest quarter, and using
the map:
, is mapped to one
of four amplitudes by rounding it off to the nearest quarter, and using
the map:
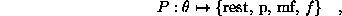
where




The second variable is mapped to a pitch set which is selected by choosing
one of five scales. A large jump between successive values causes
a change in instrumental timbre. The rapidity of the evolution of the system, along
with the abrupt numberical changes are seen as vibrating colors, and heard
as rhythms which often seem to repeat
but eventually evolve on a larger time-scale. When a new initial condition
is selected by performer V it is obvious in the visualization as a discontinuity: the appearance of a new and unrelated image. One hears this
discontinuity as an abrupt change in the melodic patterns.
6. Summary
These examples illustrate a few of the possibilities in the audification
of cellular dynamata. The choice of mappings from state-space to musical parameter space is made according to the process which is running,
and to the region of interest in parameter space. The mapping can involve
an averaging of information, to capture the complexity of the process
rather than individual trajectories. On the other hand, when one or two
trajectories are of particular interest, a mapping whose domain allows
aural distinction between a wide range of numerical values, such as pitch or
timbre, is preferable. Since the ear easily places pitches in a linear
ordering, this is a simple way to audify a relatively slowly changing,
linearly ordered sequence of numbers. If it is only the distinction between
different values that needs to be emphasized, then a subspace of timbre space can be used effectively: different instruments from some ``orchestra'' or
different values of timbre modulation, for example. For widely and rapidly
varying processes, using pitch or timbre as the range of the mapping
results in a jarring, confusing sonic representation. Using amplitude
as the target space instead allows the ear to hear longer sequences as units, and to
use rhythmic comparisons to pick out patterns in the evolution of the
structure in terms of these longer units.
These are but a few of the possibilities, and these examples should be
viewed as preliminary experiments. The use of continuous controllers which allow
navigation through parameter space in real time encourages exploration
with a variety of mappings even for one system. When particularly
beautiful areas of parameter space are discovered, and when appropriate audification
mappings have been determined, a score can be written with whatever performer
interaction is desired, be it as repeated initialization of values, movement in
parameter space, control of the mappings themselves, or the addition of other musical
lines. The rich structures of endomorphisms and cellular dynamata, most of
which are based on models of real biological or chemical systems, can
then be enjoyed by audiences without the abstraction and special vocabulary
of mathematical formulae.
Ami Radunskaya
aradunskaya@pomona.edu
Tue Dec 17 10:42:48 PST 1996
 heads, tails
heads, tails  . For Mozart's waltz,
the process (performance) outputs measures one at a time, hence the
state space is the set of all possible measures. He composed and labeled
these measures with the number 1 - 92. For a Markov process, the set
of all possible sequences of states and their relative probabilities is
described by transition probabilities: the likelihood of moving
from a given state to another. In Mozart's score it is shown that there
are only 6 measures which are allowed to follow any given measure, and
one out of these 6 measures is to be chosen ``randomly'', that is with
equal chance of any of the six occurring. Thus the transition probability of going from
measure A to measure B is zero, if B is not one of those 6 measures,
and is 1/6 if it is.
. For Mozart's waltz,
the process (performance) outputs measures one at a time, hence the
state space is the set of all possible measures. He composed and labeled
these measures with the number 1 - 92. For a Markov process, the set
of all possible sequences of states and their relative probabilities is
described by transition probabilities: the likelihood of moving
from a given state to another. In Mozart's score it is shown that there
are only 6 measures which are allowed to follow any given measure, and
one out of these 6 measures is to be chosen ``randomly'', that is with
equal chance of any of the six occurring. Thus the transition probability of going from
measure A to measure B is zero, if B is not one of those 6 measures,
and is 1/6 if it is.

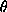 , is mapped to one
of four amplitudes by rounding it off to the nearest quarter, and using
the map:
, is mapped to one
of four amplitudes by rounding it off to the nearest quarter, and using
the map: