The $ABC$ Conjecture, formulated in $1985$ by Masser and Oesterlé asserts that for relatively prime integers $a,b,$ and $c$ such that $a+b=c$, it is rare for $rad( abc) < c$ where $rad( n) $ denotes the product of all distinct primes dividing $n$. For instance, $1+8=9$ and $rad(1\cdot8\cdot9) =6<9$. In its explicit form, the $ABC$ conjecture states that $c < rad( abc) ^{2}$. This summer we will demonstrate how the explicit form of the $ABC$ conjecture easily implies Fermat's Last Theorem, which states that the only solutions in integers to the equation $x^{n}+y^{n}=z^{n}$ satisfy $xyz=0$.
To better understand the $ABC$ conjecture, we will focus on elliptic curves, which provided the mathematical bridge for solving Fermat's Last Theorem. Shortly after the formulation, the $ABC$ Conjecture was shown to be equivalent to the modified Szpiro conjecture which roughly states that for each elliptic curve $E$, it is rare for $N_{E}^{6}<\max\!\left\{ \left\vert c_{4}^{3}\right\vert ,c_{6}^{2}\right\} $ where $N_{E}$ is the conductor of $E$ and $c_{4}$ and $c_{6}$ are invariants associated to a minimal model of $E$.
By an elliptic curve, we mean a pair $\left( E,\mathcal{O}\right) $, where $E$ is a smooth projective curve of genus one and $\mathcal{O}\in E$. A more intuitive definition of an elliptic curve is attained by considering the graph of the implicit function \[ E:y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}% \] where each $a_{j}$ is a fixed complex number. From the coefficients, we define the quantities \begin{align*} c_{4} & =a_{1}^{4}+8a_{1}^{2}a_{2}-24a_{1}a_{3}+16a_{2}^{2}-48a_{4}\\ c_{6} & =-\left( a_{1}^{2}+4a_{2}\right) ^{3}+36\left( a_{1}^{2}% +4a_{2}\right) \left( 2a_{4}+a_{1}a_{3}\right) -216\left( a_{3}^{2}% +4a_{6}\right) \\ \Delta & =\frac{c_{4}^{3}-c_{6}^{2}}{1728}\qquad\text{(we call }\Delta\text{ the discriminant of }E\text{).}% \end{align*}
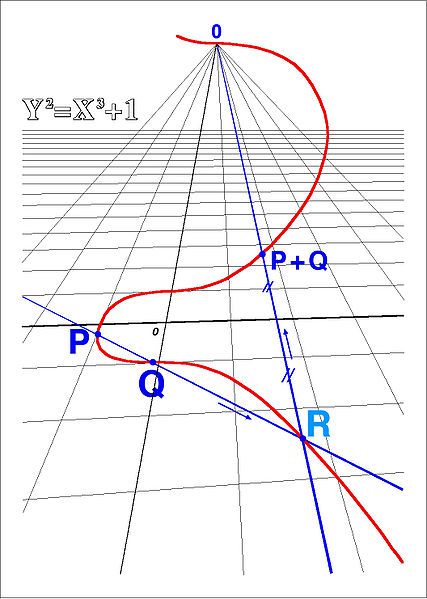
We will see that our earlier definition of an elliptic curve is equivalent via the Riemann-Roch Theorem to the following intuitive definition: By an elliptic curve $E$, we mean the graph of the implicit function \[ E:y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}% \] together with an additional point $\mathcal{O}$ which is not on the graph of $E$. The point $\mathcal{O}$ is known as the "point at infinity" and plays the role of the identity in the group structure of the elliptic curve. Indeed, in $1901$, Poincaré proved that the solutions $\left( x,y\right) $ of the implicit function together with the point at infinity forms an abelian group. The addition of points can be realized geometrically via the chord-tangent method, which we demonstrate in the special case where the coefficients are assumed to be real numbers and we restrict ourselves to those points $\left(x,y\right) \in \mathbb{R}^{2}$ which satisfy the implicit function above. Then the sum of two distinct points $P$ and $Q\ $is attained as shown below:

As part of our introduction to elliptic curves, we cover projective geometry which makes these notions precise.
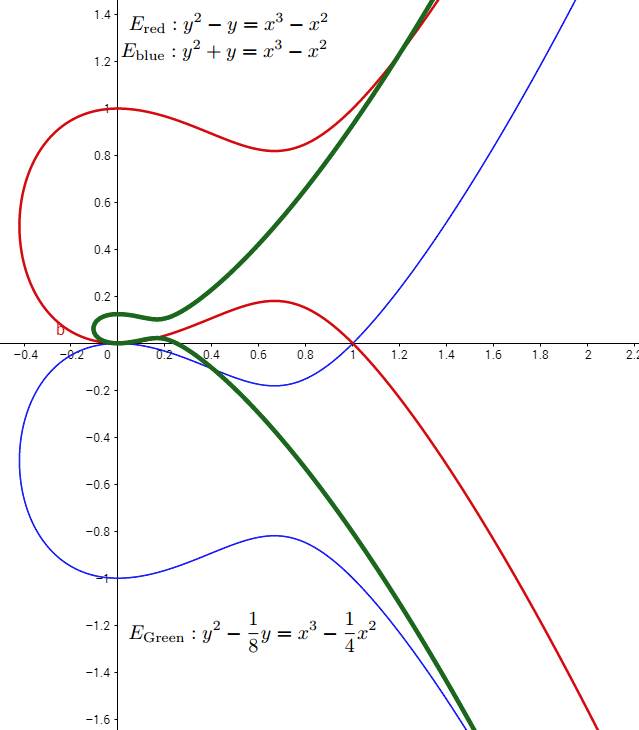
If the coefficients $a_{j}$ are rational numbers, then the elliptic curve $E$ is said to be a rational elliptic curve. We say that two rational elliptic curves $E$ and $E^{\prime}$ are $\mathbb{Q}$-isomorphic if $E^{\prime}$ can be attained from $E$ via an admissible change of variables. Intuitively, two rational elliptic curves $E$ and $E^{\prime}$ are $\mathbb{Q}$-isomorphic if $E^{\prime}$ can be attained via a translation and/or rotation of $E$. The figure below shows three different $\mathbb{Q}$-isomorphic rational elliptic curves.
Now let $E$ be a rational elliptic curve given by \[ E:y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}. \] We say $E$ is a global minimal model for $E$ if $\left( i\right) $ $a_{1},a_{2},a_{3},a_{4},a_{6},c_{4},c_{6},$ and $\Delta$ are integers and $\left( ii\right) $ $\left\vert \Delta\right\vert $ is minimal over all the $\mathbb{Q}$-isomorphic elliptic curves to $E$.
We call $\Delta$ the minimal discriminant of $E$ and denote it by $\Delta_{min}$. Moreover, the quantities $c_{4}$ and $c_{6}$ of a global minimal model of $E$ are called the associated quantities to a minimal model of $E$.
In $1975$, Hellegouarch showed that the family of elliptic curves \[ F\!\left( a,b\right) :y^{2}=x\left( x+a\right) \left( x-b\right) \] for $a$ and $b$ relatively prime integers has minimal discriminant $\Delta_{E}^{\text{min}}=\left( \frac{ab\left( a+b\right) ^{2}}{16}\right) $ if $a\equiv0\ \operatorname{mod}16$ and $b\equiv3\ \operatorname{mod}4$. In $1989$, Kraus proved a Theorem which allowed for a strengthening of Hellegouarch's work, namely:
The minimal discriminant $\Delta_{min}$ of $F\!\left( a,b\right) $ is \[ \Delta_{min}=\left\{ \begin{array} [c]{cl}% \left( \frac{a^{2}b^{2}\left( a+b\right) ^{2}}{16}\right) & \text{if }a\equiv0\ \operatorname{mod}16\ \text{and }b\equiv3\ \operatorname{mod}4\\ \left( 16ab\left( a+b\right) \right) ^{2} & \text{otherwise.} \end{array} \right. \] In $1981$, Frey gave a road map for a proof of Fermat's Last Theorem based on the family $F\!\left( a,b\right) $. In his honor, elliptic curves of the form $F\!\left( a,b\right) $ are called Frey curves.
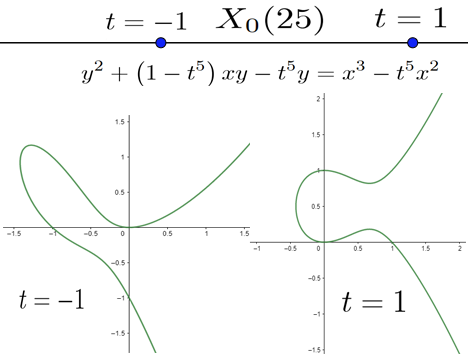
The modular curve $X_{0}\!\left( n\right) $ parameterizes isomorphism classes of pairs $\left( E,C\right) $ where $E$ is an elliptic curve and $C$ is a cyclic subgroup of $E$ of order $n$. We will focus on the genus $0$ modular curves, which correspond exactly to the case $n=1,2,\ldots,10,12,13,16,18,$ and $25$. We can view these modular curves as lines with the property that each point on the line corresponds to a pair $\left(E,C\right) $. The figure below depicts this phenomenon for the modular curve $X_{0}\!\left( 25\right)$.
The goal for the summer is to extend the classification of the minimal discriminant of the Frey curve to families of elliptic curves arising from the genus $0$ modular curves $X_{0}\!\left( n\right) $ for $n\geq3$. The first part of the project will have you tasked with constructing families of elliptic curves $E_{n}\!\left( a,b\right) $ corresponding to the modular curve $X_{0}\!\left( n\right) $. More precisely, if $\left( E,C\right) $ is a point on $X_{0}\!\left( n\right) $ with $E$ a rational elliptic curve, then $E$ is isomorphic to $E_{n}\!\left( a,b\right) $ for some integers $a$ and $b$. Once these families have been established, the focus will be on providing a classification of the minimal discriminants for each of these families.
These results will be used alongside Sage and Python to formulate conjectures on the behavior of the modified Szpiro conjecture for rational elliptic curves having a rational cyclic subgroup of order $n$.