Allow me to begin with a few definitions.
Riemann Surface. Choose a polynomial $f(x,y)$ in two variables whose coefficients are complex numbers, and let $X$ be the collection of points $P = (x_0,y_0)$ such that $f(x_0,y_0) = 0$. We say that $X$ is a Riemann surface if there are no points $P = (x_0,y_0)$ such that $$f(x_0, y_0) = \dfrac {\partial f}{\partial x}(x_0, y_0) = \dfrac {\partial f}{\partial y}(x_0, y_0) = 0.$$ For example, we will be interested in either $f(x,y) = y$, so that $X$ is the Riemann sphere; or $f(x,y) = x^3 + A \, x + B - y^2$ for some complex numbers satisfying $4 \, A^3 + 27 \, B^2 \neq 0$, so that $X$ is an elliptic curve.
Belyi Pair. Say that $X$ is a Riemann surface associated with a polynomial $f(x,y)$, and let $\beta(x,y)$ be the ratio of two polynomials whose coefficients are complex numbers. We say a complex number $z_0$ is a critical value if $z_0 = \beta(x_0, y_0)$ for some point $P = (x_0, y_0)$ satisfying $$f(x_0, y_0) = \dfrac {\partial f}{\partial x}(x_0, y_0) \, \dfrac {\partial \beta}{\partial y}(x_0, y_0) - \dfrac {\partial f}{\partial y}(x_0, y_0) \, \dfrac {\partial \beta}{\partial x}(x_0, y_0) = 0.$$ We say $(X, \beta)$ is a Belyi pair if the critical values $z_0$ of $\beta(x,y)$ are either $z_0 = 0, \, 1, \, \infty$. For example, the polynomials $f(x,y) = y$ and $\beta(x,y) = x^N$ for any positive integer $N$ form a Belyi pair for the Riemann sphere; whereas the polynomials $f(x,y) = x^3 + 1 - y^2$ and $\beta(x,y) = (y+1)/2$ form a Belyi pair for the corresponding elliptic curve.
Monodromy Group. Say that $(X, \beta)$ is a Belyi pair. A subgroup $G$ of $S_N$ is said to be a monodromy group if it is generated as follows.
For example, if $f(x,y) = y$ and $\beta(x,y) = x^N$ then $\sigma_0 = \textsf{1}$ is trivial but $\sigma_1 = (1 \, 2 \, \cdots \, N)$ and $\sigma_\infty = (N \, \cdots \, 2 \, 1)$ are $N$-cycles, so that $G \simeq \mathbb Z / N \, \mathbb Z$ is cyclic of order $N$.

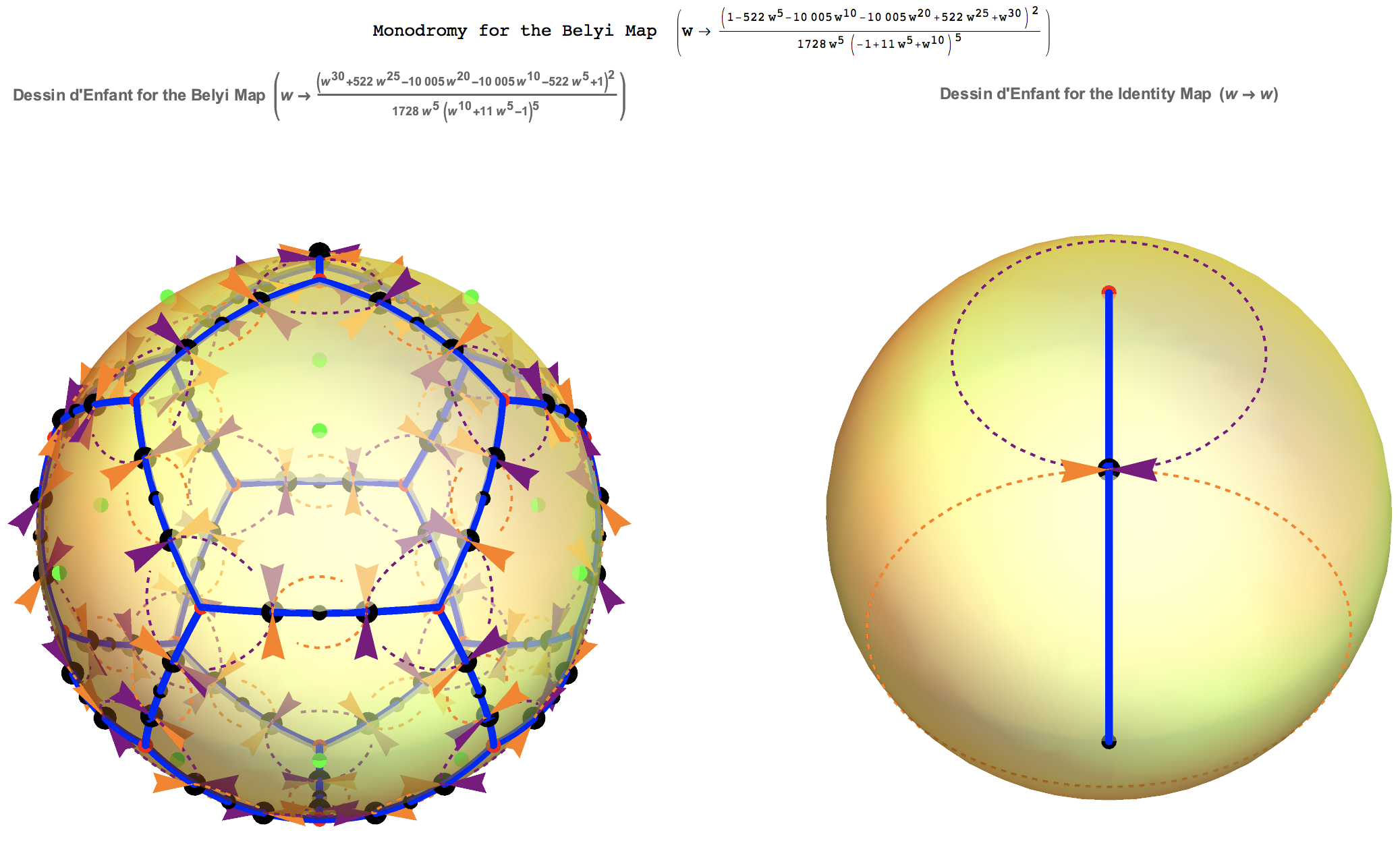
There are three main topics I would like for the students to work on this summer.
Project #1. Create a database of Belyi pairs $(X, \beta)$ along with their monodromy groups. Not many examples of Belyi maps are known, so this project seeks to compute examples and store them. For each integer $N$, there are only finitely many such pairs, and for each pair we have a unique associated subgroup of $S_N$. Compile all of these into a list. Students in this project will learn about computational commutative algebra and database management.
Project #2. Create visualizations of monodromy groups. The two loops $\gamma_{\varepsilon}$ for $\varepsilon = 0, \, 1$ trace out circles in the complex plane, and the $2 \, N$ paths $\gamma_{\varepsilon}^{(k)}$ for $\varepsilon = 0,\, 1$ and $k = 1, \, 2, \, \dots, \, N$ trace out curves on the Riemann sphere $X$. Create movies which exhibi motion on both objects, and use this to emphasize the monodromy group as permutations of the endpoints which send $\gamma_{\varepsilon}^{(k)}(0) = P_k$ to $\gamma_{\varepsilon}^{(k)}(1) = P_{\sigma_\varepsilon(k)}$. Students in this project will learn about group theory, differential equations, and visualization through computer software.