DNA segregation in Caulobacter Crescentus

C. Crescentus uses active processes to segregate its DNA. The proteins ParB and ParA are though to be important in controlling segregation. Recent experiment point to similarities between the segregation apparatus in Crescentus and the mitotic spindle in higher eukaryotic cells. We have proposed a model for chromosome segregation based on the dynamic interactios between ParB binding sites and bundles of linear ParA filaments. I am am interested in modeling various aspects of chromosome segregation in bacteria such as generation of directed motion of chromosome copies and the biochemical control of  chromosome movement directionality.

Publications:
B. Shtylla and J. P. Keener, A mathematical model of ParA filament-mediated chromosome motility in bacteria, Journal of Theoretical Biology, 2012, 307, pp. 82-95.

Polymer Brownian Motors

Biopolymer motors generate movement by using the energy of polymerization/depolymerization. In contrast to molecular motor enzymes such as dynein or kinesin, which use ATP and are recruited and reused in various locations of the cell, biopolymer motors are only assembled to perform work at specific locations and are then dissasembled. In mammalian cells, chromosomes interact with many dynamic microtubules while they move to the cell equator. We have proposed a mathematical model for how kinetochore filaments can be coupled with dynamic microtubules to generate movement. We find that the resulting force-velocity relations are non-linear and that motility characteristics depend on the individual kinetochore filament binding strengths.  I am interested in modeling the dynamic interactions between various kinetochore proteins and microtubules. In general, I am interested in the collective behavior of active and passive molecular motor assays. The details of interactions between these cellular machines are important for the formation of eukaryotic mitotic spindles and the proper progression of cell division.

Publications:
J. P. Keener and B. Shtylla. A mathematical model of force generation by flexible kinetochore-microtubule attachments*, Biophysical Journal, 106 (5), pp. 998-1007. abstract
*Article featured on the cover of the March 04 issue of the Biophysical Journal and in "Modeling kinetochores: when form and function becomes art" on the Biophysical Society Blog

A. Sharma*, B. Shtylla* and D. Chowdhury. Distribution of lifetimes of kinetochore-microtubule attachments:interplay of energy landscape, molecular motors and microtubule (de-)polymerization, 2013, (to appear in Physical Biology).

B. Shtylla and J. P. Keener. A mathematical model for force generation at the kinetochore-microtubule interface. SIAM Journal on Applied Mathematics, 2011, 71(5), pp. 1821-1848. abstract, pdf


Mechano-chemical control of Mitotic events in higher Eukaryotes

During mitosis, cells have to ensure that precisely half of the replicated DNA is allocated to each daughter cell. Accuracy is achieved with the help of a complex biochemical regulatory network, which keeps track of the microtubule attachment status of each moving chromosome during division. Even a single lost attachment will put division into a hold! The surveillance of a chromosome requires that a cell know not only the attachment status but also the amount of force that each chromosome is sustaining due to its interactions with the mitotic spindle. We have shown that mechanochemical feedbacks are important in assuring proper mitosis progression. I am interested in modeling the mechanisms mediating the integration of biochemical and mechanical signals during mitosis in mammalian cells.

Publications:
A. Matzavinos, B. Shtylla, Z. Voller, S. Liu, and M. A.J. Chaplain. Stochastic modelling of chromosomal segregation: Errors can introduce correction, 2013, (in revision).

B. Shtylla and J. P. Keener, A mechanomolecular model for the movement of chromosomes during mitosis driven by a minimal kinetochore bicyclic cascade, Journal of Theoretical Biology, 2010, 263(4): 455-70. abstract, pdf

Full list of publications

Undergraduate Research Opportunities:


There are various venues for participation in research for students that are interested in mathematical biology:

1. Research assistant (academic year or summer): contact me directly if interested.

2. 5C SURP or HHMI funded fellows can work on problems in mathematical biology with me here.

3. Senior Thesis in Mathematics as part of the senior exercise, if you are a double major looking for a primer on interdisciplinary research this might be a great option. It is preferable that you contact me during your Junior year to explore options. Some generic instructions about senior thesis in mathematics are here and for interdisciplinary projects here. I am happy to discuss Mathematics Thesis research projects, especially if you are a junior math major at Pomona college. Some examples of thesis projects I have supervised are listed below.

Senior Thesis:

2013-2014

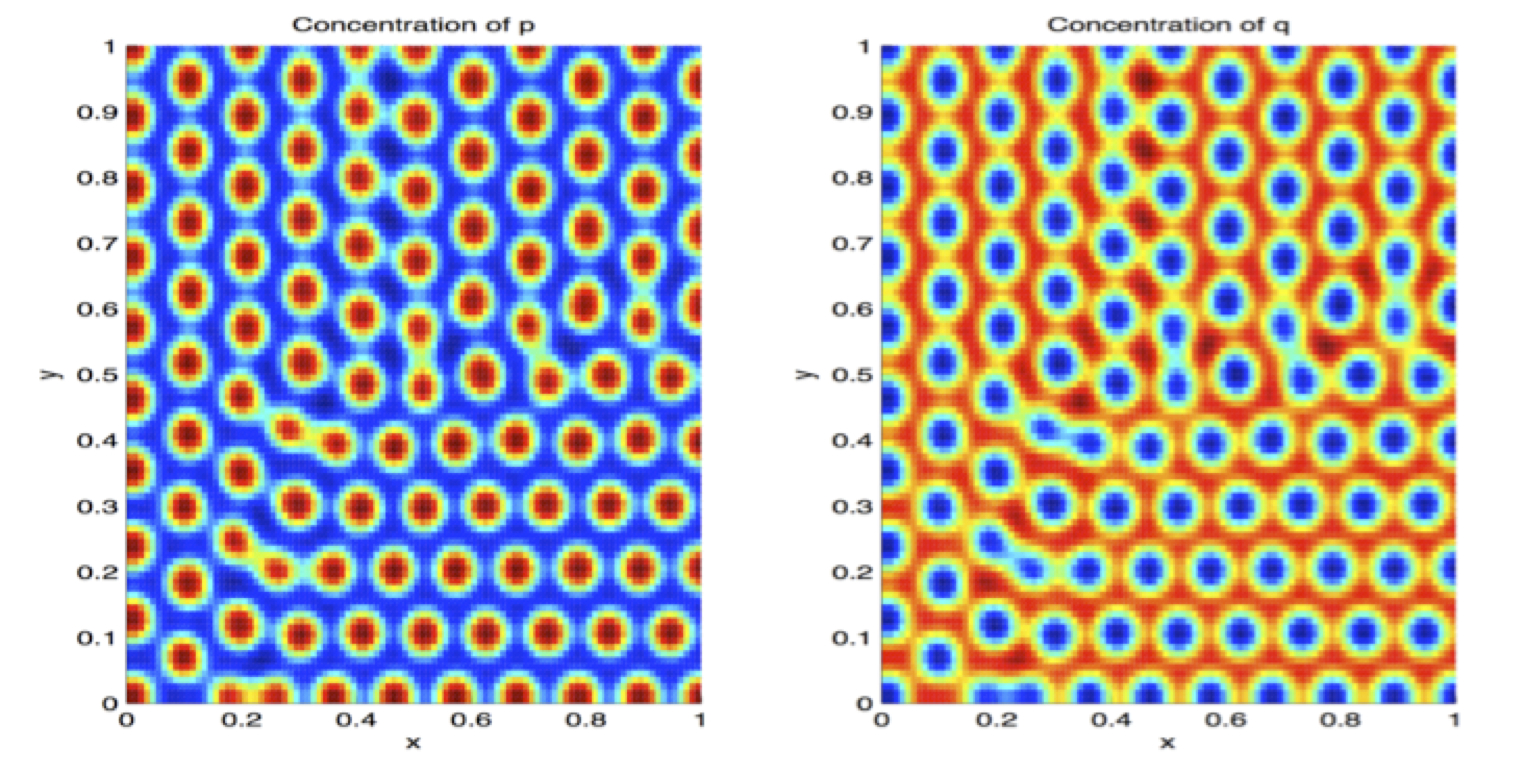
  • Emily Meyer, Pomona '14: Turing Patterns for spatial-temporal signalling. Emily is working on reaction-diffusion models for protein localization in dividing cells.

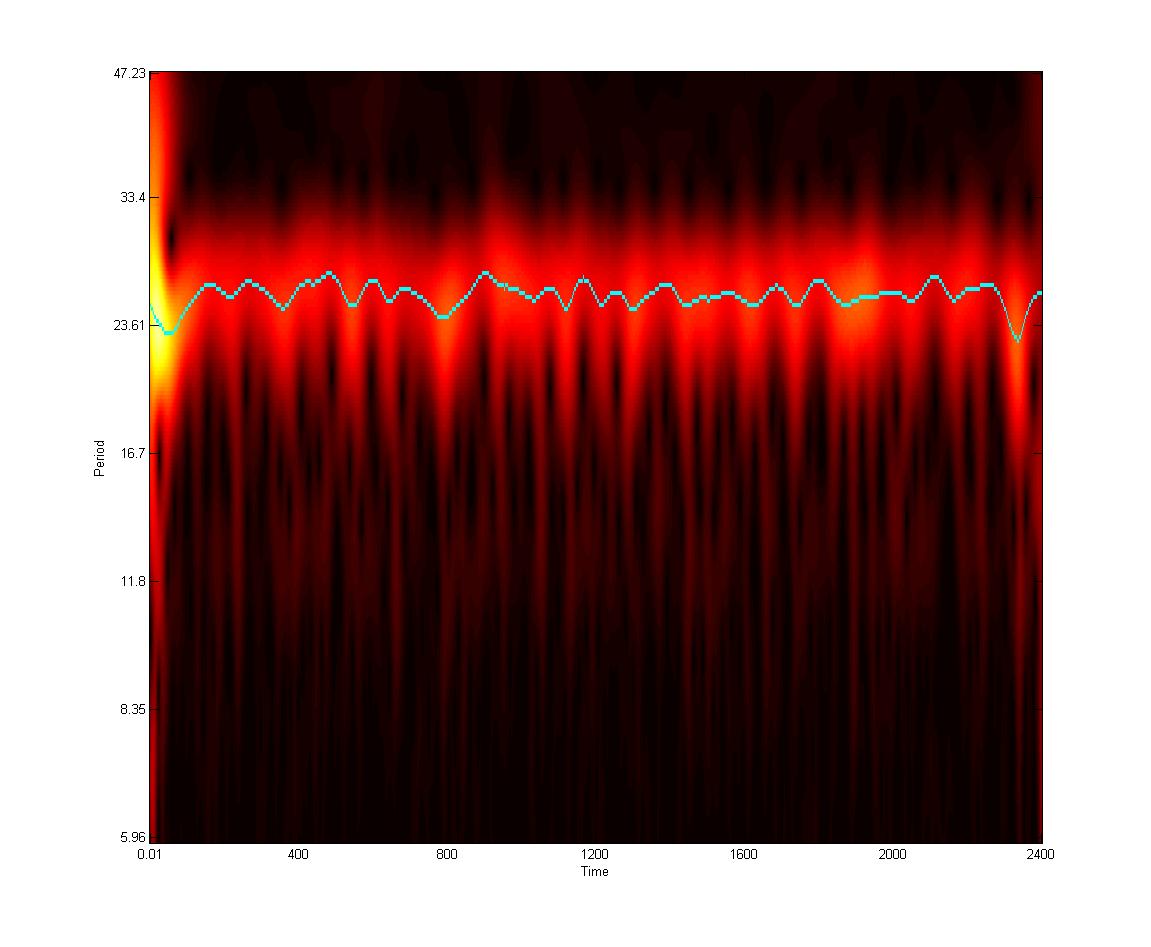
  • David Morgens, Pomona '14. Noisy Clocks: Stochastic Modeling of Circadian Rhythms. David is working on analysis of stochastic fluctuations in order to identify functional biological modules.

  • Kyle Roskamp, Pomona '14. Understanding and Applying Graph Ranking to Gene Ontologies.
  • Kevin Guttenplan, Pomona '14. Mathematical Modeling of Axon Guidance at the  Drosophila melanogaster  Midline.

A full schedule of our exciting thesis presentations and topics can be found here . If you want to find out more about this, come and join us for the talks!

Current Research Students:

  • Matt McDermott, Havery Mudd College '14: A computational model for cell mechanics in early C. elegans development.

Previous Research Students:

  • Sangeeta Warrier, Mt. Holyoke College '15.

Current Research Funding:

National Science Foundation RUI (2012-2015)

"Mathematical Modeling of chromosome segregation and organization in bacteria"