The following are research projects I'm actively working on with students during the academic year. I am always looking for students! Click on the links to learn more about these projects. History of African Americans in the Mathematical Sciences I'm looking to hire undergraduates to help maintain the MAD Pages. Students working on this project do not need to have a background in the mathematical sciences. This project is ongoing, and takes place during the academic year. Belyi Maps and the Dessin Explorer I'm looking for students to write code to assist with development of a software suite called Dessin Explorer. Students working on this project must have a background in computer programming; a background in mathematics is preferred but not necessary. This project is meant to compliment work done as part of PRiME, although work will takes place during the academic year. Ranks of Elliptic Curves via Class Groups TBA. I'm happy to chat about these in more detail. The easiest way to contact me is by scheduling a time with Calendly. History of African Americans in the Mathematical Sciences Background In 1997, Scott Williams (SUNY Buffalo) founded the website Mathematicians of the African Diaspora. It has since become widely known as the MAD Pages. According to a 2019 blog written by Williams for the American Mathematical Society, As a child I was struck by the emphasis, within the general American culture, upon achievements in the Sports/Entertainment Industry as indications of success. Within the African American subculture, those indications are even stronger - just consider the winners of the NAACP Image Awards among other celebrations. On the rare occasion a scientist has won an award, there has been a limitation to the medical field. In addition, where it concerns successes in mathematics and the sciences, I discovered much incorrect or misconstrued information available in texts and especially on the web. Williams built the site over the course of 11 years, creating over 1,000 pages by himself as a personal labor of love. The site features more than 700 African Americans in mathematics, computer science, and physics as a way to showcase the intellectual prowess of those from the Diaspora. Williams provided profiles of these individuals, detailing their education, their journey within mathematics thus far, and their accomplishments. In addition to the hundreds of profiles, Williams also created numerous pages discussing Black history within the mathematical sciences, and presented data on the demographics of Black people in the mathematical sciences at the time. Since its creation, the MAD Pages have received more than 20 million visitors, and provided immeasurable inspiration and validation to many Black mathematicians and students. Scott Williams retired from SUNY Buffalo in 2008. He was concerned with who would take over the site he had spent 11 years building. In 2010, there was a town hall meeting about the future of the MAD Pages which took place at the Conference for African American Researchers in the Mathematical Sciences (CAARMS) in Baltimore. Williams informed the crowd that he was concerned the Pages would be lost as there was no guarantee that the SUNY Buffalo Math Department would continue to host the site. Don King (Northeastern University) took on this challenge, but found the task too overwhelming for one person. In 2017, at the National Association of Mathematicians's (NAM) annual Banquet in Atlanta, Don King had a short conversation with Edray Goins (Pomona College) and Asamoah Nkwanta (Morgan State University). The three decided to place the charge of updating the MAD Pages under the auspices of NAM since Goins was president at the time. The Ad Hoc committee to update the MAD Pages was co-chaired by Don King (Northeastern University) and Asamoah Nkwanta (Morgan State University). Other committee members were Terrence Blackman (Medgar Evers College), Ron Buckmire (then NSF), NAM President Edray Goins (then Purdue University), Monica Jackson (American University), Talitha Washington (Howard University/NSF), and web developer John Weaver (Varsity Software). Based on a proposal from Varsity Software, the committee worked in stages to preserve the legacy of the MAD Pages. Goals and Objectives The first African American to receive a doctorate in mathematics, Elbert Frank Cox, did so in 1925; the first African American woman, Euphemia Lofton Haynes, received her doctorate in 1943. In 1968, data from National Science Foundation (NSF) states that there were 22,937 doctorates awarded in the United States across all disciplines, with 971 in mathematics and computer science. Just 9 of those went to African Americans mathematicians. In 2016, there were 3,957 doctorates granted in mathematics and computer science, but just 78 went to African American mathematicians. While the percentage of Blacks receiving doctorates in the mathematical sciences has doubled in the past 50 years -- from 0.93% to 1.97% -- this is a far cry from 12%, the percentage of Blacks living in the United States. Still, a crude estimate puts the total number of Blacks who have ever earned a doctorate in the mathematical sciences at under 5,000 individuals. Until recently, there was no database to keep track of who these recipients were, to learn their stories, or to showcase their work. Just as one can tell the stories of Elbert Frank Cox and Euphemia Lofton Haynes, one should be able to tell the individual stories of the nine African Americans who graduated in 1968. Prof. Goins envisions the MAD Pages as the main historical record of these 5,000 individuals. Currently, there are approximately 800 names in the database, and Prof. Goins plans to expand to include the names of every African American to receive a doctorate in the mathematical sciences. Prof. Goins wishes to hire undergraduates to help maintain the MAD Pages. The objectives towards that goal are as follows: Add missing names. Students will add names of Black mathematicians which are missing from the database. This information will include (a) basic biographical information including birthdate and photograph, (b) doctoral thesis information such as title and year of completion, and (c) most recent employment and contact information. Write biographies. Students will write biographies for those names currently in the database which are missing such a narrative. These biographies would compliment -- not simply repeat -- those which may exist on similar sites such as the "Biographies of Women Mathematicians'' at Agnes Scott College, "Mathematically Gifted & Black", and the "MacTutor History of Mathematics Archive" at the University of St. Andrews. Links to existing media. Students will add links from external media such as (a) personal and professional websites, (b) videos of talks and interviews, and (c) links to other biographical sites such the "Biographies of Women Mathematicians", "Mathematically Gifted & Black", and the "MacTutor History of Mathematics Archive". MR Number. Students will search the American Mathematical Society's MathSciNet to find the Mathematical Reviews Number (MR Number) associated to names in the MAD Pages database. The MAD Pages links with MathSciNet so that profiles in the database will have the most up-to-date information on the author's publications. Students working on this project do not need to have a background in the mathematical sciences. This project is ongoing, and takes place during the academic year. References Edray Herber Goins and Amy Oden. Diary of a Black Mathematician: Finding Community. In "Count Me In: Community and Belonging in Mathematics". AMS MAA Press, Classroom Resource Materials, Volume 68 (2022); 241 pages. Edray Goins, Don King, Asamoah Nkwanta, and John Weaver. Mathematicians of the African Diaspora -- Updated Site. Edray Herber Goins and Amy Oden. Updated "MAD Pages" Website to be Unveiled October 9. Notices of the American Mathematical Society, Volume 68, Number 2 (February 2021), pages 254-255. DOI: https://doi.org/10.1090/noti2224. Edray Goins Three Questions: The Journey of One Black Mathematician. Notices of the American Mathematical Society, Volume 65, Number 2 (February 2018), pages 144-147. DOI: http://dx.doi.org/10.1090/noti1637. Rya Jetha. Pomona and Cal Poly students team up to document Black contributions to mathematics. The Student Life (March 10, 2022). Susan E. Kelly, Carly Shinners, and Katherine Zoroufy. Euphemia Lofton Haynes: Bringing Education Closer to the "Goal of Perfection". Notices of the American Mathematical Society. Volume 64, Number 9 (2017). Pages 995-1003. DOI: http://dx.doi.org/10.1090/noti1579. Erica Walker, Scott Williams, and Robin Wilson. An Existence Proof: The Mathematicians of the African Diaspora Website. AMS inclusion/exclusion blog. January 31, 2019. Talitha M. Washington. Evansville Honors the First Black Ph.D. in Mathematics and His Family. Notices of the American Mathematical Society. Volume 55, Number 5 (2008). Pages 588-589. Scott W. Williams. Mathematicians of the African Diaspora -- Legacy Site. 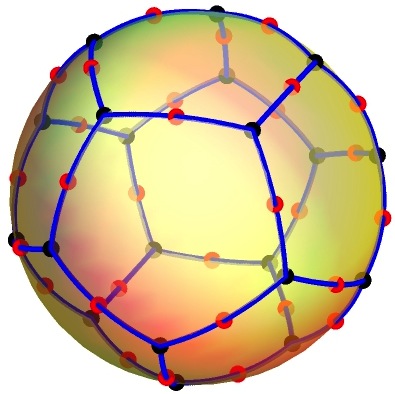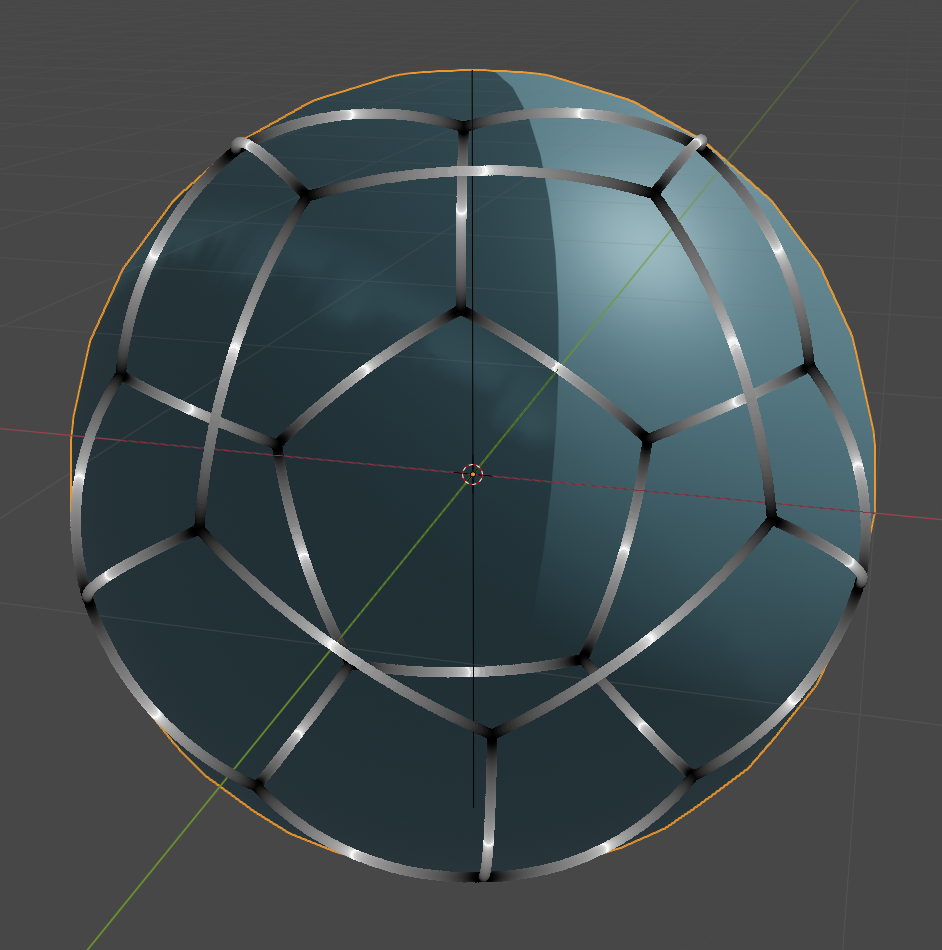Belyi Maps and the Dessin Explorer Background Let \(S\) be a compact, connected Riemann Surface. For example, \(S = \mathbb P^1(\mathbb C) \simeq S^2(\mathbb R)\) may be the Riemann Sphere, or \(S = E(\mathbb C) \simeq (\mathbb R/\mathbb Z) \times (\mathbb R/\mathbb Z)\) may be a torus associated to an elliptic curve \(E\). It is well-known that \(S\) is a curve, that is, can be defined by a single equation \(f(x,y) = 0\) for some polynomial \(f(x,y) = \sum_{ij} a_{ij} \, x^i \, y^j\) having complex coefficients \(a_{ij}\). Andre Weil proved in 1956 that one can choose these coefficients to lie in a number field if there exists a meromorphic function \(\beta: S \to \mathbb P^1(\mathbb C)\) with at most three critical values; Gennadii Vladimirovich Belyi proved the converse to this in 1979. For this reason, we call \(\beta\) a Belyi map. It is easy to show that \( z_0 \in \mathbb P^1(\mathbb C)\) is a critical value if and only if \(z_0= \beta(P_0) \) for a point \(P_0 = (x_0, y_0)\) such that the function \(f(x,y)\) and the Jacobian \( \partial(f,\beta)/\partial(x,y) = \bigl( \partial f/\partial x \bigr) \, \bigl( \partial \beta/\partial y \bigr) - \bigl( \partial f/\partial y \bigr) \, \bigl( \partial \beta/\partial x \bigr) \) simultaneously vanish. Examples of such maps can be found through the L-functions and Modular Forms Database (LMFDB). In 1984, Alexander Grothendieck proposed a way to create a bipartite graph from such a map. Say the critical values are \( \{ z_0, \, z_1, \, z_\infty \} \subseteq \mathbb P^1(\mathbb C) \); replacing the Belyi map with the composition \( \gamma \circ \beta \) in terms of the Moebius transformation \( \gamma(z) = \bigl( (z_1 - z_\infty) \, (z - z_0) \bigr) / \bigl( (z_1 - z_0) \, (z - z_\infty) \bigr)\), we may assume \(z_0 = 0 \), \(z_1 = 1\), and \(z_\infty = \infty \). Denote the preimages \(B = \beta^{-1}\bigl( \{0\} \bigr)\) as the "black vertices", \(W = \beta^{-1}\bigl( \{1\} \bigr)\) as the "white vertices", \( F = \beta^{-1}\bigl( \{ \infty \} \bigr)\) as the "midpoints of faces", and \(\beta^{-1}\bigl( [0,1] \bigr)\) as the "edges"; then the bipartite graph \(\beta^{-1} \bigl( [0,1] \bigr) \subseteq S \hookrightarrow \mathbb R^3 \) is called a Dessin d'Enfant. According to Grothendieck: I do not believe that a mathematical fact has ever struck me quite so strongly as this one, nor had a comparable psychological impact. This is surely because of the very familiar, non-technical nature of the objects considered, of which any child's drawing scrawled on a bit of paper (at least if the drawing is made without lifting the pencil) gives a perfectly explicit example. To such a dessin we find associated subtle arithmetic invariants, which are completely turned topsy-turvy as soon as we add one more stroke. Let \(e_P\) denote the ramification index a point \(P \in B \cup W \cup F = \beta^{-1}\bigl( \{0, \, 1, \, \infty \} \bigr)\); this is the number of edges incident to the vertex \(P\). The degree sequence of a Belyi map is a multiset \(\mathcal D = \bigl \{ \bigl \{ e_P \, \bigl| \, P \in B \bigr \}, \ \bigl \{ e_P \, \bigl| \, P \in W \bigr \}, \ \bigl \{ e_P \, \bigl| \, P \in F \bigr \} \bigr \}\). The Riemann-Hurwitz Formula / Handshaking Lemma asserts that the genus \(g(S)\) of the Riemann surface \(S\) can be determined from this combinatorial data. That is, \(\deg \beta = \sum_{P \in B} e_P = \sum_{P \in W} e_P = \sum_{P \in F} e_P = |B| + |W| + |F| + \bigl( 2 \, g(S) - 2 \bigr)\). The degree sequence can be determined just by counting the number of edges surrounding the "black vertices", "white vertices", and "midpoints of faces". But which degree sequences correspond to Belyi maps? Adolf Hurwitz answered this question in 1891. Fix a positive integer \( N \), and say that we have a multiset \(\mathcal D = \bigl \{ \bigl \{ e_P \, \bigl| \, P \in B \bigr \}, \ \bigl \{ e_P \, \bigl| \, P \in W \bigr \}, \ \bigl \{ e_P \, \bigl| \, P \in F \bigr \} \bigr \}\) of three partitions of \(N\) for some indexing sets \(B\), \(W\), and \(F\) such that \(N = |B| + |W| + |F| + (2 \, g - 2)\). Then \(\mathcal D\) is the degree sequence for some Belyi map \(\beta: S \to \mathbb P^1(\mathbb C)\) on a compact, connected Riemann surface of genus \(g(S) = g\) and degree \(\deg \beta = N\) if and only if there exist three permutations \( \sigma_0, \, \sigma_1, \, \sigma_\infty \in \text{Sym}(N) \) such that (i) each permutation \(\sigma_0\), \(\sigma_1\), and \(\sigma_\infty\) is a product of disjoint cycles with cycle type \(\bigl \{ e_P \, \bigl| \, P \in B \bigr \}\), \(\bigl \{ e_P \, \bigl| \, P \in W \bigr \}\), and \(\bigl \{ e_P \, \bigl| \, P \in F \bigr \}\), respectively; (ii) the composition \(\sigma_0 \circ \sigma_1 \circ \sigma_\infty = 1\) is the identity permutation; and (iii) the group \(G = \left \langle \sigma_0, \, \sigma_1, \, \sigma_\infty \right \rangle\) is transitive subgroup of the symmetric group \(\text{Sym}(N)\). One can determine the permutations \( \sigma_0, \, \sigma_1, \, \sigma_\infty \in \text{Sym}(N) \) by (1) labeling the edges of the Dessin d'Enfant from 1 through \(N \) and (2) reading off these labels by moving counterclockwise around each vertex \(P \in B \cup W \cup F = \beta^{-1}\bigl( \{0, \, 1, \, \infty \} \bigr)\). The group \(\text{Mon}(\beta) = G = \left \langle \sigma_0, \, \sigma_1, \, \sigma_\infty \right \rangle \) generated by these permutations is the monodromy group. Goals and Objectives Prof. Goins is looking to write a computer program in Mathematica which computes these quantities. He would like to make this software, called the Dessin Explorer, freely available on his website. There are four objects of interest that this software would compute: Degree Sequences. For each positive integer \(N \) and each non-negative integer \(g \), we may compute all multisets \(\mathcal D = \bigl \{ \bigl \{ e_P \, \bigl| \, P \in B \bigr \}, \ \bigl \{ e_P \, \bigl| \, P \in W \bigr \}, \ \bigl \{ e_P \, \bigl| \, P \in F \bigr \} \bigr \}\) of three partitions of \(N\) such that \(N = |B| + |W| + |F| + (2 \, g - 2)\). We wish to determine those degree sequences which correspond to permutations \( \sigma_0, \, \sigma_1, \, \sigma_\infty \in \text{Sym}(N) \) as in Hurwitz's theorem. While slow, Mathematica can determine such permutations. Can we create a database indexed by \(N\) and \(g\) of such degree sequences \(\mathcal D \)? Belyi Maps. Given such a degree sequence \( \mathcal D \), Hurwitz's theorem asserts that a Belyi map \(\beta: S \to \mathbb P^1(\mathbb C)\) should exist. When \(S = \mathbb P^1(\mathbb C) \simeq S^2(\mathbb R)\) has \( g = 0 \), we can choose \( f(x,y) = y \) and write our Belyi map in the form $$\beta(x) = {\displaystyle \prod_{P \in B} \left( \dfrac {b_P \, x - a_P}{b_P \, a_1 - a_P \, b_1} \right)^{e_P}} \biggr/ {\displaystyle \prod_{P \in F} \left( \dfrac {b_P \, x - a_P}{b_P \, a_1 - a_P \, b_1} \right)^{e_P}} = 1 - \displaystyle \prod_{P \in W} \left( \dfrac {b_P \, x - a_P}{b_P \, a_0 - a_P \, b_0} \right)^{e_P} \biggr/ \displaystyle \prod_{P \in F} \left( \dfrac {b_P \, x - a_P}{b_P \, a_0 - a_P \, b_0} \right)^{e_P}$$ for some points \( P_0 = (a_0 : b_0) \in B\) and \(P_1 = (a_1 : b_1) \in W\). Can we write code which will determine the points \(P = (a_P : b_P) \in \mathbb P^1(\mathbb C)\) by solving a system of equations? Can we implement homotopy continuation to do this? Can we perform a similar trick for any genus \(g \)? Monodromy Groups. Given a Belyi map \(\beta: S \to \mathbb P^1(\mathbb C)\) defined on a compact connected Riemann surface \(S\) defined by a polynomial \(f(x,y)\), we can determine the monodromy group \(\text{Mon}(\beta) = \left \langle \sigma_0, \, \sigma_1, \, \sigma_\infty \right \rangle \) by looking at loops \( p: [0,1] \to S \) around \( \varepsilon = 0\) and \(1\) which are solutions \( p(t) = \bigl( x(t), \, y(t) \bigr)\) to the system of first order ordinary differential equations $$ \dfrac {dx}{dt} = - 2 \pi i \, (\beta - \varepsilon) \, \dfrac {\partial f/\partial y}{ \partial(f,\beta)/\partial(x,y) } \quad \text{and} \quad \dfrac {dy}{dt} = +2 \pi i \, (\beta - \varepsilon) \, \dfrac {\partial f/\partial x}{ \partial(f,\beta)/\partial(x,y) } \quad \text{where} \quad \dfrac {\partial(f,\beta)}{\partial(x,y)} = \dfrac {\partial f}{\partial x} \, \dfrac {\partial \beta}{\partial y} - \dfrac {\partial f}{\partial y} \, \dfrac {\partial \beta}{\partial x}. $$ Can we write code in Mathematica which will determine the permutations \( \sigma_0, \, \sigma_1, \, \sigma_\infty \in \text{Sym}(N) \) from a Belyi map \(\beta\)? Can we implement using Runge-Kutta to numerically solve this equation? Dessin d'Enfants. Given a Belyi map \(\beta: S \to \mathbb P^1(\mathbb C)\) we would like to visualize the bipartite graph \( \beta^{-1} \bigl( [0,1] \bigr) \subseteq S\). When \(S = \mathbb P^1(\mathbb C) \simeq S^2(\mathbb R)\) has \( g = 0 \), we can embed \( S \hookrightarrow \mathbb R^3\) via stereographic projection. That is, can view the Dessin d'Enfant in 3-dimensions by considering the image of the point $$\left( \dfrac {2 \, x(t)}{x(t)^2 + y(t)^2 + 1}, \dfrac {2 \, y(t)}{x(t)^2 + y(t)^2 + 1}, \, \dfrac {x(t)^2 + y(t)^2 - 1}{x(t)^2 + y(t)^2 + 1} \right) \quad \text{where} \quad \dfrac {dx}{dt} = - \dfrac {\partial f/\partial y}{ \partial(f,\beta)/\partial(x,y) }, \quad \dfrac {dy}{dt} = + \dfrac {\partial f/\partial x}{ \partial(f,\beta)/\partial(x,y) };$$ as \( 0 \leq t \leq 1 \), where initially \( f \bigl( x(0), y(0) \bigr) = 0\) and \( \beta \bigl( x(0), \, y(0) \bigr) = \varepsilon\) for \(\varepsilon = 0\) or \(1\). Can we implement this so that we can generate the Dessin d'Enfant quickly, perhaps by numerically solving the differential equations? Can we visualize this Dessin using a 3D viewer? Can we even print the Dessin using a 3D printer? Students working on this project must have a background in computer programming; a background in mathematics is preferred but not necessary. This project is meant to compliment work done as part of PRiME, although work will takes place during the academic year. References Tesfa Asmara, Edray Herber Goins, Erik Imathiu-Jones, Maria Maalouf, Isaac Robinson, and Sharon Sneha Spaulding. Critical Points of Toroidal Belyi Maps. ArXiv (December 2022). Gennadii Vladimirovich Belyi; translated by Neal Koblitz. Galois Extensions of a Maximal Cyclotomic Field. Mathematics of the USSR-Izvestiya. Volume 14, Number 2 (1980). Pages 247-256. DOI: https://doi.org/10.1070/IM1980v014n02ABEH001096. Jacob Bond. On the Computation and Composition of Belyi Maps and Dessins d'Enfants. Doctoral Thesis. (May 2018). Edray Goins, Kevin Iga, Jordan Kostiuk, and Kory Stiffler. The Signed Monodromy Group of an Adinkra. ArXiv (September 2019). Ernesto Girondo and Gabino Gonzalez-Diez. Introduction to Compact Riemann surfaces and Dessins d'Enfants. London Mathematical Society Student Texts, Volume 79, Cambridge: Cambridge University Press (2012). ISBN 978-0-521-74022-7. DOI: https://doi.org/10.1017/CBO9781139048910. Leonardo Zapponi. What is a Dessin d'Enfant? Notices of the American Mathematical Society. Volume 50, Number 7 (August 2003). Pages 788-789. Ranks of Elliptic Curves via Class Groups Background TBA Goals and Objectives References